이 글은 정보 전달이 아닌, 개인적으로 공부하고 배운 내용을 정리하여 피드백을 주고 받기 위한 목적으로 작성되었습니다. 그러므로 정확하지 않은 정보 및 생각들이 난무할 수 있음을 유의해주세요.
오늘의 주제: cartesian coordinate system
<나는 왜 이 주제를 업로드하는가?>
- ocw 강의를 듣는데, 자꾸 Gilbert Strang 교수님이 칠판에 x-y 평면을 그리신다.
- 이전부터 데카르트 좌표계(cartesian coordinate system)의 발명이 얼마나 위대한 것인지 잘 와닿지 않았다.
이 글을 작성하는 데는 wikipedia_cartesian coordinate system을 참고했다. 딱 한 문장을 참고했는데, 그건 바로...
"A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length."
그 중에서도 밑줄 친 부분만 참고했다..! 왜냐면 그 부분이 가장 인상깊었다. 그래서 그 부분의 문장 구조(?)를 분석해봤다.
perpendicular라는 것은 찾아보니 '직교'를 뜻한다. 글에서는 'lines'에다가 'perpendicular'와 'oriented'라는 수식어를 붙였다. 물론, 'fixed'라는 수식어도 있지만, 그 부분은 이 글에서는 논외로 하려한다.
그 다음으로, "distances"라는 표현에는 'signed'라는 수식어가 붙었다. 사실 글을 적기전 생각을 정리해봐도, 이 signed라는 표현이 뭔가 독특한 감이 오기는 하지만, 그마저도 아주 흐릿해서, 뭐라고 말로 정리하기가 힘들다. 그래서 이부분도 논외로 하려한다.
아무튼, 그래서 나의 질문은 다음으로 정리할 수 있다.
- 질문1) 두 개의 oriented lines는 왜 직교(perpendicular)해야 하는가? 만약에 직교하지 않는다면 어떤 일이 발생할까..?
- 질문2) 글에서 언급된 oriented line을 축(axis)라고 표현해도 될까?(우선, 이 부분은 참이라고 가정하고 글을 이어나가려고 한다.)
- 질문3) 두 개 이상의 축이 존재할 때(각각 axis1, axis2라 하겠다), axis1과 axis2의 값이 모두 0이 되는 지점을 교차하게 만들면, 직선간의 각도가 어떻든 어쨌든 평면이 생성될 것이다. 만약, 그 평면에 임의의 점 P를 잡는다면, P의 값은 axis1에 대한 값도 있을 것이고, axis2에 대한 값도 있을 것이다. 그 각각의 값들은 어떻게(음.. 아마도 기하학적인 방법으로) 추론할 수 있을까?
질문 3이 내가 가장 궁금한 것인데, 그냥 중학교 때 배우는 흔한 좌표평면을 그려보면 다음과 같을 것이다.
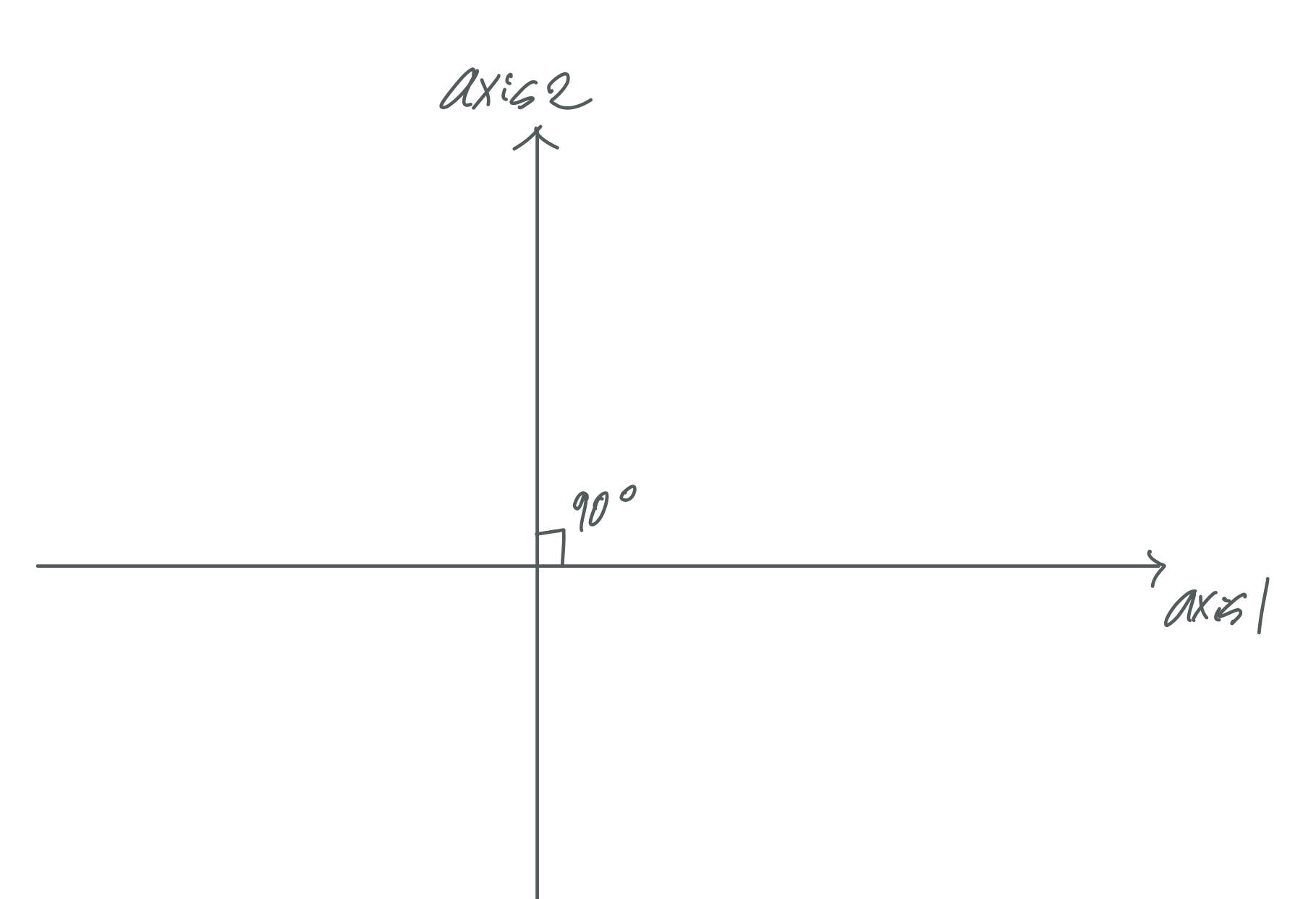
그리고 그 때 어떤 점의 각 축에 대한 값들을 찾을 때, 학교 선생님들은 흔히 다음과 같이 설명했다.

위 이미지는 P의 좌표값을 찾기 위해 각 축(axis1, axis2)에 수선의 발(각각 H1, H2)를 내렸다. 두 개의 축 모두 그 위에 있는 점에 대응하는 값들이 존재한다. 따라서, H1에 대응하는 값을 찾으면, 그것이 P의 axis1에 대한 값이 되고, H2에 대응하는 값을 찾으면, 그것이 P의 axis2에 대한 값이 된다.
여기서 질문이 또 생겨난다..
좌표평면에서 왜 어떤 점의 좌표값을 찾기 위해 반드시 그 축에 수선의 발을 내려야 하는 걸까? 뭔가 되게 쓸데없는 질문인 것 같기도 하지만.. 좀 비스듬히 그어서 좌표값을 찾으면 안되나(...)하는 생각이 든다.
그리고 그 다음으로는 이런 질문도 생겨난다...
평면상에서 예컨대 역시 바로 위 그림에서, P를 axis1 축에 평행하게 움직이면, axis2값은 변하지 않는다. 나는 뭔가 P의 기하학적 변화가 분명 있음에도 불구하고, 어떤 축에 대해서는 전혀 변화가 없을 수 있다는게 신기하다. 근데 나는 신기한데, 이게 다른 사람도 공감할 수 있는 신기함인지는 모르겠다 ㅠㅠ
바로 위 질문은 사실 다음과 같은 상황에서 P의 움직임이 axis1과 axis2에 어떤 변화의 영향을 미치는지..어떻게 파악할 수 있을까?라는 궁금증으로 이어졌다.
다음과 같은 상황이란, 바로.. 두 좌표축이 직교하지 않는 경우를 말한다.

바로 위의 이미지와 같은 경우, P의 움직임이 존재하되, axis2에는 값의 변화가 없도록 할려고 하면 어떻게 해야 될까? 그런 것도 궁금하다.
아무튼 이것으로 포스팅을 마무리하려고 한다.
'수학' 카테고리의 다른 글
| 수학 카테고리 글 곧 업로드 예정입니다 (0) | 2020.03.13 |
|---|---|
| 블로그 작성 빈도 (0) | 2020.02.09 |
| [공부 일지] vector space의 항등원/역원의 유일성 (2) | 2020.02.03 |
| 공부 일지_2020.1.31 (0) | 2020.02.01 |
| 연립일차방정식을 푸는 두 가지 방식 (0) | 2020.01.30 |
